라쏘? 로지스틱? 회의에서 당당하게, 수식없이 기초개념부터
이전편 : 랜덤포레스트가 뭐길래? 회의에서 당당하게, 수식없이 알아보자
분류문제에서 많이 쓰이는 로지스틱 회귀분석. 회귀분석은 어디서 들어본 것 같은데, 로지스틱?
logistic 병참(학)의
logistics (많은 사람·장비가 동원되는 복잡한 작업의) 실행 계획
[네이버 사전]
병참, 실행계획이라니.. 군대에서 쓰는 단어인가? 물류라고 들어본 거 같은데..
게다가 라쏘, 릿지라니..
lasso 1. 올가미 밧줄(소말 등을 잡기 위해 밧줄 한쪽 끝을 고리 모양으로 묶은 것)
ridge 1. 산등성이, 산마루 2. (산등성이처럼) 길쭉하게 솟은 부분 3. (대기압의) 기압 마루
[네이버 사전]
영어 단어 뜻만으로는 도저히 무슨말인지 모르겠는데, 검색해 보면 온갖 복잡한 수식밖에 없는 것 같다.
빅데이터와 인공지능 시대가 와서 일반 직장인들도 머신러닝 관련 단어를 많이 듣게 되었다. 직접 분석할 필요는 없기 때문에 복잡한 수식을 알 필요는 없지만 도대체 어떤 이야기를 하는 것인지를 알고 싶은 사람들을 위해서,
가장 간단한 방법 중 하나인 회귀분석을 통해 지도학습이라는 머신러닝의 개념을 알아보고, 현업에서도 많이 쓰이는 라쏘, 릿지 회귀까지 알아보도록 하자.
왜 저런 방법을 쓰는지 어떤 개념이 녹아들어 있는지를 알면, 마케터나 기획자로서 어떤 데이터가 필요한 것인지, 분석의 결과 값을 어떻게 해석해야 좋을지 인사이트를 얻을 수 있을 것이다.
목적은 비전공자, 비전문가에게 최소한 알아야할 기본적인 내용을 전달하는 것이다. 짧은 글에 많은 내용을 담다보니 빠진 부분, 그냥 넘어간 부분이 많을 수 있음을 염두해 두자.
이전 편 랜덤포레스트와 달리, 회귀분석류들은 결과 자체가 함수의 형태로 표현되기 때문에 수식을 안쓸 수가 없긴 하다. 하지만 최대한 글과 그림으로 설명해 보도록 하겠다.
- 지도학습의 개념
- 회귀분석과 로지스틱 회귀
- 라쏘, 릿지가 나오게 된 배경
- 조정값 튜닝이란.
순으로 알아보자.
지도학습이란?
머신러닝, 즉 기계학습은 우리 인간이 학습을 하는 방법을 빗대서 붙인 표현이다. 우리가 세상을 배우는 데는 크게 구분하면 아래의 두 가지 방법을 사용한다고 한다.
1) 가르쳐주지 않아도 아는 것
갓난아기 때부터 관찰을 통해 우리는 유사함과 다름을 느끼면서 스스로 학습을 한다. 움직이는 것과 움직이지 않는 것, 사람과 동물 등을 구분하는 것이 그 예일 것이다.
2) 정답을 배우면서 학습해 가는 것
반면에 부모 등 누군가가 답을 계속 알려주면, 정답에 가까워지면서 배우는 방법이 있다. 난생 처음 '강아지'라는 단어를 들은 아이는, 비슷한 크기의 모든 동물을 강아지라고 말한다. 부모가 다시 '이 작은 동물은 강아지가 아닌 고양이'라는 것을 알려주면, 점점 강아지와 고양이를 구분하는 방법을 학습하게 된다. 이렇게 사회가 알려준 정답과 내가 인식하는 세상을 비교해가면서 배우는 것이다.
이렇게 사람이 학습을 하는 과정을 흉내내어 머신러닝에서는 1)과 같은 방법을 비지도 학습Unsupervised Learning, 2)와 같은 방법을 지도 학습Supervised Learning이라고 한다.
이번 글의 주제 중 하나인 2)지도학습의 비지도학습과의 가장 큰 차이점은 정답이 있다는 것이다.
잠시 학창시절로 돌아가보면, 중요 개념을 배운 후 연습문제를 풀어본다. 답이 맞으면 제대로 이해했구나 하게 되고, 틀리면 잘못 이해했으니 다시 개념을 배우는 과정을 거친다. 그리고 시험을 통해 실전문제를 푼다.
마찬가지로 설명변수(개념)와 그 정답을 포함하고 있는 데이터(연습문제)를 가지고, 새로운 문제(시험)를 풀 수 있는 모형을 만들어 내는 것이 지도학습 머신러닝 방법이다.
회귀분석
그래서 컴퓨터에게 어떻게 가르칠까? 어디서 들어보기는 한거 같은 회귀분석의 예제를 보면서 알아보자.
지도학습의 두 가지 세팅
보통 지도학습에서 데이터는 다음과 같이 설명변수와 답의 쌍을 준비한다. 데이터 로우row가 00개 라는 이야기는 이런 쌍이 00개 있다는 말이다.
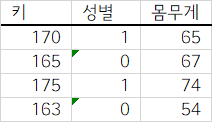
키와 성별로 몸무게를 예측해 보자.
이렇게 데이터가 준비되면, 데이터 외에 두 가지 준비를 한다.
1. 예측을 어떻게 할건지?
우리가 가진 데이터로 현실 세계를 가장 잘 설명할 수 있는 모양을 가정한다. 모형Model 이라고 한다. 시험 문제를 풀기 위해서 어떤 개념들을 알면 좋을지, 공부할 개념들을 정하는 것이라고 생각할 수 있겠다.
현실의 우리들은 여러 개념들을 뇌에서 복잡한 상호작용으로 엮어서 문제를 풀지만, 컴퓨터에게는 컴퓨터가 알 수 있는 방식으로 모양을 구성해 주어야 한다. 풀고자 하는 문제가 의사결정나무 모양으로 예측이 될 거라고 생각할 수도 있고, 딥러닝처럼 복잡하게 예측이 될 거라고 생각할 수 있다.
회귀분석에서는 아래와 같은 모양으로 현실이 예측이 될 거라고 생각한다.
몸무게는 키와 성별에 따라 비례관계를 가질 것
컴퓨터가 알아들을 수 있도록, 수식 같기도 아닌것 같기도 한 표현으로 하면 아래와 같다.
몸무게 = 키*(키의 비중) + 성별*(성별 비중)
+ 오차
이런 설정에서는 몸무게는 이렇게 추정하면 된다.
> 추정몸무게 = 키*(키의 비중) + 성별*(성별 비중)
오차는 몸무게를 잴 때 생기는 측정오차나, 키나 성별로 설명되지 않는 오차 같은 것이라고 생각하면 되겠다. 오차는 데이터 상에서 우리가 알 수 없는 것이므로 추정몸무게에는 오차가 없는 것을 확인하도록 하자.
여기서 (키의 비중)과 (성별 비중)을 찾아내면, 실전 문제를 예측 할 수 있는 모형이 완성된다. 이런 값들을 회귀계수Coefficient 라고 한다. 이 값을 찾으려면 어떻게 해야 할까.
2. 예측을 잘한다는 것이 어떤건지?
키의 비중과 성별의 비중을 찾기 위해서, 예측을 잘하는 것이 무엇인가 조건을 정해야 하는데, 이를 목적함수Objective/Loss Function 라고 한다. 단순히 문제를 맞힌건지 틀린건지도 포함하지만, 우리가 시험을 대비할 때 단순 과목별 총합 점수를 높이는 것을 목표로 할 때가 있고, 과목별 표준점수 합을 높이는 것을 목표로 할 때가 있는 것 처럼 문제와 상황에 따라 이 목적함수는 달라질 수 있다.
기본적으로 회귀분석에서 우리가 원하는 것은
실제 몸무게와 추정한 몸무게가 차이가 없어야 한다.
이를 컴퓨터가 알아듣게 하기 위해서, 쉽게 실제 몸무게에서 추정몸무게를 뺀 값을 차이라고 정의하면 되겠다.
예측의 차이 = (실제 데이터에서 몸무게 - 우리가 추정한 몸무게)
이 예측의 차이(오차)의 총점, 즉 데이터의 모든 쌍에서 오차를 합한 값을 최소로 하는 계수(키의 비중, 성별 비중)를 찾으면 된다. 이것이 회귀분석에서 쓰는 목적함수이다.
실제로는 여러이유로, 우리가 분산을 계산할 때처럼 오차의 '제곱'을 최소화하도록 목적함수를 구성한다.
어떻게 찾을까
무식하게 모든 값을 탐색해가다보면 가장 차이값을 적게 하는 값을 찾을 수도 있겠다. 설명변수 개수가 적고, 요즘 같이 컴퓨팅 성능이 좋을 때는 불가능한 일은 아닐 수도 있지만, 회귀분석은 컴퓨터라는 것이 없던 시절 나온 방법이라 사람 손으로도 계산할 수 있는 방법을 찾았다.
최소값을 구하기 위해 고등학교 때 들어보았던, 미분과 적분 중에 미분 을 사용한다. (미분 적분 그거 배워서 어디에 쓰나?!) 미적분을 배우지 않은 분들을 위해 간단히 설명하자면, 보통 어떤 적절한 함수의 최대나 최소값을 구하고자 할 때 미분값=0 의 방정식을 이용한다.
값은 컴퓨터가 계산해 주지만, 중요한 것은 목적함수를 최대로 하거나 최소로 하는 값들을 찾는 것이 지도학습의 가장 큰 축이라는 것이다.
간단한 회귀분석결과는 엑셀 산점도 차트에서 '추세선' 을 그려보면 된다. 아래는 엑셀에서 몸무게 = 기본값 + 키(키의비중) 의 모형으로 추세선을 그린 그림이다. 가로(x)는 키, 세로(y)는 몸무게이다.
로지스틱 회귀분석
2개 클래스를 분류하는 문제의 경우 목적변수(답)를 1,0 으로 놓고 모형을 학습하여 결과값을 '1이 될 확률'로 생각하면 된다. 그런데 분류 문제에서는 회귀분석 보다는 로지스틱 회귀라는 방법을 많이 사용한다.
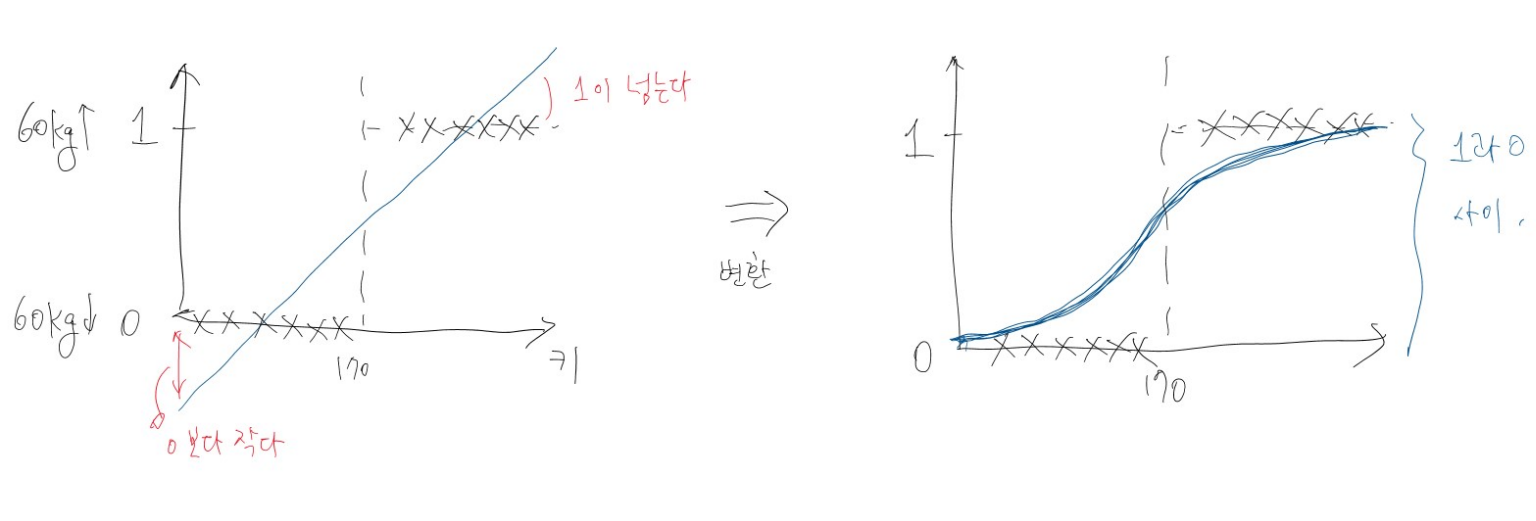
몸무게 예측 문제에서 몸무게 자체가 아닌 몸무게가 '60Kg 이상인지 여부'를 예측하는 경우라고 해보자. 아래그림과 같이 키와 (몸무게>60)을 일반 회귀분석으로 구하게 되면, 0과 1을 넘어가는 예측 값이 생긴다. 확률로 해석하기에는 문제가 있다.
그래서 로지스틱 함수라고 하는 '껍데기'를 목적변수에 씌워 0과 1사이로 값이 나올 수 있도록 변환해준다. 참고로 아래와 같은 모양이다.
$ log( {\text{몸무게>60 확률}\over \text{몸무게<60 확률}} ) $ = 회귀식 = (키의비중)*키 + (성별비중)*성별
이렇게 변환하면 몸무게>60일 확률은 0과 1사이가 되어 확률로 해석할 수 있게 된다. (참고로 log안에 들어가는 부분(1확률 / 0확률)을 오즈odds 라고 한다. 도박이나 의료 분야에서 많이 쓰는 지표로, 일어나지 않을 확률보다 일어날 확률이 얼마나 큰지를 보는 지표다.)
나머지는 일반 회귀분석과 거의 비슷하다. 계수추정이 조금 어렵긴 하지만 계산은 컴퓨터가 해준다. 중요한 것은 목적함수를 최대/최소로 한다는 것.
라쏘, 릿지 회귀
이제 회귀분석에서 한발짝 더 나아가서, 라쏘LASSO와 릿지Ridge 에 대해서 알아보자. 회귀분석은 여러분야에서 많이 보이는 방법이라서 익숙한 편이지만, 이런 용어들은 낯설것인데 라쏘나 릿지가 나오게된 배경부터 살펴보자.
변수의 수가 늘어나면
자꾸 풀던 문제집만 풀면 새로운 문제를 봤을 때 못 풀게 되는 경우가 많다. 중요한 개념보다 문제에만 특수한 부분들이 더 많이 학습되기 때문이다. 같은 문제집을 수십번 풀다보면 문제 번호만 봐도 답이 보이게 될 것이다. 이게 문제가 된다. 학습을 할 때 '문제풀이'가 아니라 '개념'을 배우라고 하지 않던가!
이와 비슷하게 머신러닝에서도, 모형에서 쓰이는 설명변수 수가 늘어나면, (문제에 특수한 부분들이 늘어날 가능성이 있지만) 주어진 데이터에선 예측을 더 잘하게 된다.
설명변수 없이 그냥 결과 값만 가지고 있으면(설명변수 0개), 몸무게를 예측하기 위해서 가장 오차가 적은 방법은 평균(58.3)이다.
설명변수 하나를 추가해서 키를 알고 있다면? (설명변수 1개), 몸무게=(키-92)*0.85로 그냥 평균으로 예측하는 것보다 잘 맞는다. 역시성별을 알게되면, 키*0.3 + 성별*13.3 으로 더 잘 맞는다.
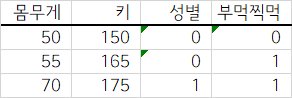
이제 변수를 하나 더 추가해서 이사람의 (부먹찍먹 여부) 를 추가해보자(설명변수 2개). 몸무게 = (키-100)*1 + 성별*10 + 부먹찍먹*(-10) 로 하면 100% 답이 맞다!
부먹찍먹 여부로 몸무게를 예측할 수 있다니!
'부먹찍먹' 같은 변수를 모형에 사용하는 것은, 문제집을 풀 때 1단원의 1번은 5, 2번은 4, … 이렇게 외우는 것과 같다. 다른 문제집을 풀 때 잘 못풀게 되는 것 처럼, 이런 '부먹찍먹' 같은 변수를 학습한 모형을 실전 문제에 적용하게 되면 문제가 생긴다. 이런 것을 과적합overfitting 문제라고 한다.
머신러닝에서 중요한 주제 중 하나는 이런 과적합을 방지하는 방법이다.
과적합 문제 뿐 아니라, 변수의 수가 늘어나면 당연히 모형을 인간이 이해하고 설명하는게 어려워지는 문제점도 있다.
예시에서는 당연히 누가봐도 상관이 없어 보이는 부먹찍먹 변수를 모형에서 제거하고 학습을 하면 되지만, 소득, 가족구성원 등 관계가 애매한 다른 변수들이 있을 수도 있고, 현실의 문제에 있는 적게는 수십개, 수백개의 변수를 어떻게 모두 판단을 할 수 있을까?
'이건 이 문제에만 특수한 것이고, 중요한 개념은 이거야.' 라는 것을 컴퓨터가 배워가는 한 가지 방법이 변수선택 또는 축소 방법이다. 릿지, 라쏘 방법은 이런 용도로 사용을 한다.
그래서 이렇게 조정하자
앞에서 살펴보았던 지도학습의 설정을 바꿔서 해결해보자.
현실 세계를 설명하는 우리의 모형은 그대로 두고, 목적은 아래와 같이 바뀔 것이다.
예측 오차는 최소로 했으면 좋겠는데, 설명변수도 너무 많지않으면 좋겠다.
이를 반영하여 릿지나 라쏘에서 사용하는 목적함수는 아래와 같다
목적함수 = (차이의 합) + (조정값)*(추정된 계수들의 크기)
왼쪽이 원래 우리가 목적함수로 정했던 '차이'이고, 두번째가 추가되었다.
왜 추정된 계수들의 크기가 중요한지는
설명변수의 영향이 크다 $ \approx $ 계수 크기가 0이 아니고, 계수의 크기가 크다
설명변수가 제외된다 $ \approx $ 설명변수의 영향이 적다 $ \approx $ 계수의 크기가 0에 가깝다
를 생각해 보면 된다. 추정된 계수의 크기가 0에 가까울 수록 해당 설명변수의 영향도가 줄어들게 되고 0이 되면 변수가 아예 제거된다.
이제 새로운 목적함수를 최소로 하는 계수들을 찾으면 된다. 이 때 설명변수들이 늘어나면 차이값이 줄어들게 되므로 왼쪽이 줄지만, 계수들의 크기는 커지기 때문에 오른쪽이 늘어난다. 서로 trade-off 관계가 성립하게 되는 것이다. 그래서 오른쪽을 벌칙penalty 항이라고 한다. 벌칙항을 추가함으로써 너무 많은 설명변수를 방지하는 것이다. 결론적으로 주어진 데이터를 맞히는 데는 약간의 예측오차가 발생하지만, 이를 감수하면서 새로운 문제를 더 잘 맞힐 수 있도록 과적합을 방지하는 것이다.
문제를 풀 때 하나의 문제를 맞히는 것도 중요하지만, 그 문제만 외우지 말고 문제의 근본에 있는 중요한 개념을 배워나가는 것이라고 생각하면 되겠다.
튜닝?
위의 벌칙항에서 조정값 부분을 보자. 조정값이 크면 벌칙이 세지고, 그 만큼 설명변수의 숫자는 더 적게 나오는 결과가 나올 것이다. 작으면 반대로 더 많은 설명변수들이 모형에 포함될 것이다. 이 조정값은 어떻게 정하면 좋을까?
조정값을 여러번 조정하면서 새로운 문제를 가장 잘 맞히는 숫자를 찾게 된다. 분석가들이 하는 이런 작업을 튜닝Tuning 이라고 한다.
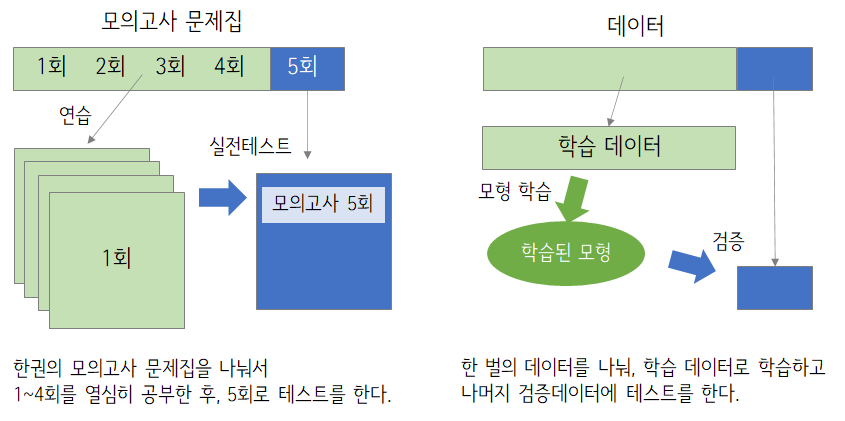
다시 학교 때로 돌아가서, 5회로 이루어진 모의고사 문제집 한권을 우리가 가진 데이터라고 해보자. 보통 4회의 모의고사를 열심히 공부해서 잘 맞히는 방법을 배운 후에 나머지 안풀어본 1회 문제를 풀어서 이게 진짜 실력인지 확인하는 과정을 거친다.
비슷하게 우리가 모형을 학습시킬 때, 데이터를 두 부분으로 나누어 4회의 학습데이터Training Set로 학습을 시키고 안풀어본 1회의 검증데이터Validation Set로 실제 상황을 빗대어서 잘 맞히는지 확인해보는 과정을 거친다.
릿지와 라쏘의 차이
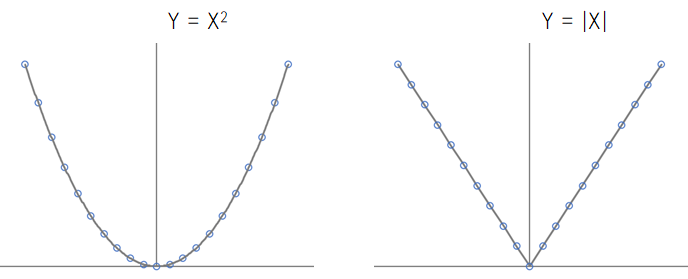
둘의 차이는 벌칙항의 모양에 있다. 릿지의 경우는 벌칙항이 제곱의 형태( 계수2의 합)이고, 라쏘의 경우는 절대값의 형태( |계수|의 합)이다.
제곱 과 절대값의 차이를 보자. 어려운 수식이나 그래프를 제외하고 설명하자면, 아래 그래프처럼 하나는 0 주위에서 둥글둥글하고, 하나는 각이 졌다.
느낌적인 느낌으로 릿지(제곱)는 설명변수들의 계수를 둥글둥글하게 (0에 가깝게) 줄이는 것이고, 라쏘는 설명변수들의 계수를 각지게 없애는(0으로 만드는) 것이라고 생각하면 되겠다.
릿지는 그래서 모든변수들을 사용하는 모형이 생긴다. 단지 영향이 큰 변수보다는 영향이 적은 변수들의 영향력을 0에 가깝도록 줄이는 것이다. 라쏘는 반면에 각진 부분에서 변수의 영향을 0으로 만들어버린다.
이런 이유로 성능은 모든변수를 사용하는 릿지가 라쏘보다 좀더 낫고, 반면 라쏘는 변수의 수를 줄여주기 때문에 해석력이 좀 더 좋다고 할 수 있다.
역시 모든 것은 trade-off 이므로, 과적합을 줄인 예측력이 중요하다면 릿지, 변수의 숫자를 줄여서 해석력을 얻고자 한다면 라쏘를 사용하면 된다.
마무리
지도학습의 개념부터 라쏘, 릿지 회귀까지, 머신러닝의 기본 설정부터 과적합, 학습-검증 데이터의 분리까지 알아보았다. 요약하자면
- 지도학습은 데이터에 정답이 포함되어 있다.
- 모형과 목적함수를 설정하고, 목적함수를 최소로 하는 값을 찾는다.
- 로지스틱 회귀는 확률(0,1사이)로 만들기 위해 목표변수를 변환하는 회귀분석의 종류다.
- 변수가 늘어나면 풀던 문제는 잘풀지만, 새로운 문제는 못푸는 과적합 문제가 생긴다.
- 릿지와 라쏘는 목적함수에 벌칙항을 추가해서 과적합을 방지한다.
- 데이터를 훈련, 검증 데이터로 나누어, 새로운 문제를 잘 푸는 가장 좋은 모형을 찾는다.
보통의 직장인들이 직접 모형을 학습시키는 업무를 하지 않더라도, 분석가, 솔루션 업체와의 회의에서 이러한 용어들이 많이 나온다.
그때마다 데이터에 대한 질문 -물론 무엇보다 가장 중요한 질문이다- 만 하지 말고, 다음의 사항들에 대한 호기심을 가지면 더 좋은 분석결과, 더 좋은 솔루션을 얻을 수 있을 것이다.
목적함수는 무엇인가? 우리 문제와 맞나?
변수선택은 어떻게 했나? 없애는게 맞나 줄이는게 맞나?
과적합의 문제는 없나? 데이터를 어떻게 나눠서 학습시켰나?
참고로 처음에 사전에서 찾아본 영어단어를 설명하면,
- 로지스틱Logistic 이라는 용어는 프랑스어 logistique 에서 왔다고 하는데, 처음 소개한 학자가 이유를 밝히지는 않았다고 한다. 예상으로는 Log의 반대라는 의미로 붙였거나, 그리스 수학의 분파 중 하나에서 따왔다는 이야기도 있다. 1)
- 라쏘LASSO는 least absolute shrinkage and selection operator 의 줄임말로 아마 올가미로 중요한 변수들을 잡아챈다는 중의적 의미를 노리고 만든 것 같다.
- 릿지Ridge는 릿지 방법을 사용한 추정계수가 원래 회귀계수들을 중심으로 '등고선ridge'을 그리기 때문에 붙여진 이름이다.
Reference
shrinkage methods
An Introduction to Statistical Learning, Gareth M. James 外, Springer, 2014
The Elements of Statistical Learning, Trevor Hastie 外, Springer, 2001
Computer Age Statistical Inference, Bradley Efron 外, Cambridge University Press, 2016
More
| 2021/09/24 06:30 | |
| 2020/06/18 11:34 | |
| 2020/06/07 14:03 | |
| 2020/05/28 10:29 | |
| 2020/05/12 09:03 | |
| 2020/05/07 09:27 | |
| 2020/04/29 10:52 | |
| 2020/04/20 11:12 | |
| 2020/04/16 15:23 | |
| 2020/04/15 07:21 | |
| 2020/04/11 01:41 | |
| 2020/04/08 06:49 | |
| 2020/04/01 00:55 | |
| 2020/03/21 13:43 | |
| 2020/03/20 11:53 | |
| 2020/03/15 11:11 | |
| 2020/03/07 07:35 | |
| 2020/03/01 16:09 | |
| 2020/02/29 04:52 | |
| 2020/02/29 04:52 | |
| 2020/02/29 04:52 | |
| 2020/02/29 04:52 | |
| 2020/02/29 04:52 | |
| 2020/02/29 04:49 | |
| 2020/02/06 12:58 |


Discussion