Review on BPR: Bayesian Personalized Ranking from Implicit Feedback, Rendle et al.

—

### Explicit Feedback : user's preference of item itself

eg. '1-5 score' of movies, 'like/dislike' in video streaming service

### Implicit Feedback : user behavior which reflects their interest 'indirectly'

eg. purchase history, click, view, etc.

- only positive feedback observations are available.
- non-observed user-item pairs = real negative feedback + missing value
—

Algorithm = model + objective function + optimization
###

### objective function = BPR-OPT
### optimization = LEARN_BPR
#
### model = ?

—

* $U$ : set of all users, $I$ : set of all items
* $S \subseteq U \times I$ : implicit feedback
* $>_u \subset I^2$ : personalied total ranking of all items

properties of total order: $\forall i,j,k \in I$
(totality) : $\text{if } i \neq j \text{, then } i >_u j \text{ or } j >_u i$
(antisymmetry) : $\text{if } i>_uj \text{ and } j>_ui \text{, then } i = j$
(transitivity) : $\text{if } i>_uj \text{ and } j>_uk \text{, then } i>_u k$

* $I_u^+:=\{i \in I : (u,i) \in S\}$, $U_i^+:=\{u \in U : (u,i) \in S\}$

—

* use item pairs as training data
* optimize for correctly ranking item pairs instead of scroing single items

### Training data

$D_s := \{ (u,i,j) | i \in I_u^+ \text{ and } j \in I\setminus I_u^+ \}$ : training set

$\Rightarrow$ $(u,i,j)\in D_s$ means user u is assumed to prefer i over j : $i>_uj$

### Advantages
1. can treat both positive and negative pairs and missing values
2. training data is created for the actual objective of ranking

—

Bayesian formulation : maximize posterior probability

$$ P(\Theta|>_u) \propto p(>_u|\Theta)p(\Theta) $$
$\Theta$ : parameter vector of an arbitrary model class

—

set $X_{uij} = I(i>_uj)$,
then $X_{uij} \sim Bernoulli(p_{uij})$ where $p_{uij} = p(i>_uj)$

for all user analysis, assume that each $(u,i,j) \in D_s$ are independent.

$$\prod_{u\in U}p(>_u|\Theta) = \prod_{(u,i,j)\in D_s}p_{uij}^{x_{uij}}(1-p_{uij})^{1-x_{uij}} =\prod_{(u,i,j)\in D_s}p_{uij}$$

—

with setting $p(i>_uj|\Theta) := \sigma(\hat{x}_{uij}(\Theta))$, where $\sigma (x) := {1 \over 1+ \exp(-x)}$
and prior $p(\Theta)$ as normal distribution $N(0,\lambda_{\Theta} ^{-1}I)$

$$ \begin{matrix} \text{BPR-OPT} &:=& \ln \prod_{u\in U}p(\Theta|>_u) \\ &=& \ln \prod_{u\in U}(p(>_u|\Theta)p(\Theta) \\ &=& \sum_{(u,i,j)\in D_s} \ln\sigma(\hat{x}_{uij}(\Theta)) + \ln p(\Theta) \\ &=& \sum_{(u,i,j)\in D_s} \ln\sigma(\hat{x}_{uij}(\Theta)) - \lambda_{\Theta} \lVert\Theta\rVert^2 \end{matrix} $$
where $\lambda_{\Theta}$ are model specific regularization parameters.

※ form of MLE with $l_2$-regularization

—

$$ \begin{matrix} AUC &=& {1 \over|U|}\sum_{u\in U} AUC(u) \\ &=& {1 \over|U|}\sum_{u\in U} {1 \over |I_u^+||I\setminus I_u^+|} \sum_{i\in I_u^+} \sum_{j \in I\setminus I_u^+} \delta(\hat{x}_{uij}>0) \\ &=& \sum_{(u,i,j)\in D_s}z_u \delta(\hat{x}_{uij}>0) \end{matrix} $$
where $z_u$ is normalizing constant.

### compare to the BPR-OPT : they only differ in the loss function
* non-diferentiable $\delta(x>0)$ is approximated by $\ln \sigma(x)$

—

### gradient descent

$$ {\partial \text{BPR-OPT} \over \partial \Theta} = \sum_{(u,i,j)\in D_s} {-\exp(-\hat{x}_{uij}) \over 1+\exp(-\hat{x}_{uij})} \cdot {\partial \over \partial\Theta}\hat{x}_{uij} - \lambda_\Theta \Theta$$

1. Full GD

• too large training data : $O(|S||I|)$ triples
• the skewness in the training pairs : the dominating class affect largely
• regularization is difficult as the gradients differ much

2. Stochastic GD

• good approach for skew problem
• but, order of training data traversed is crucial
  • in typical method (item-wise or user-wise), there are so many consecutive updates on the same user-item pair

$\Rightarrow$ bootstrap sampling with replacement

—

Many model predict a real number $\hat{x}_{ul}$ per user-item pair $(u,l)$

To learn such model with BPR,
Decompose the estimator $\hat{x}_{uij}$
> $$ \hat{x}_{uij} := \hat{x}_{ui}-\hat{x}_{uj} $$

※ use same model, but optimize it against another criterion.
(difference of two prediction instead of single number)

—

$X = [x_{ui}]$ is approximated by two low-rank matrices $W:|U| \times k$ and $H:|I|\times k$

$$ \hat{X} := WH^t $$
$$ \hat{x_{ui}} = \langle w_u, h_i \rangle= \sum_{f=1}^k w_{uf} \cdot h_{if} $$
$$ w_u : \text {row in }W \text{, describing user } u $$
$$ h_i : \text {row in }H \text{, describing item } i $$

—

$\Rightarrow \Theta = (W,H)$

$${\partial \over \partial\theta}\hat{x}_{uij} = \begin{cases} (h_{if}-h_{jf}) & \text{if } \theta = w_{uf}, \\ w_{uf} & \text{if } \theta = h_{if}, \\ -w_{uf} & \text{if } \theta = h_{jf}, \\ 0 & \text{else} \end{cases}$$

$\lambda_W$ $\lambda_{H^+}$ $\lambda_{H^-}$ : regularization for each $\Theta$

—

$$ \hat{x}_{ui} = \sum_{l \in I_u^+\text{ and }l \neq i} c_{il} $$
where $C:I \times I$ is the symmetric item-correlation/similarity matrix.

$\Rightarrow \Theta = C$

$${\partial \over \partial\theta}\hat{x}_{uij} = \begin{cases} +1 & \text{if } \theta \in \{c_{il}, c_{li} \} \text{ and } l \in I_u^+\text{ and }l \neq i, \\ -1 & \text{if } \theta \in \{c_{jl}, c_{lj} \} \text{ and } l \in I_u^+\text{ and }l \neq j, \\ 0 & \text{else} \end{cases}$$

$\lambda_{+}$ $\lambda_{-}$ : regularization for each $\Theta$

—

### Weighted Regularized MF (WR-MF)
implicit

$$ \sum_{u\in U} \sum_{i\in I} c_{ui}(\langle w_u, h_i \rangle - 1)^2 + \lambda\lVert W \rVert _f^2 + \lambda\lVert H \rVert _f^2 $$

1. this optimization is on instance level (one item) instead of pair level (two items) as BPR.
2. this optimization is a least square - correspond to the MLE for normally distributed random variables.

1. But item prediction is actually not a regression(quantitative),

but a classification (qualitative) one

1. so the logistic optimization is more appropriate.

—

### Maximum Margin MF (MMMF)
explicit

$$ \sum_{(u,i,j) \in D_s} max(1- \langle w_u,h_i-h_j \rangle ) + + \lambda_w \lVert W \rVert _f^2 + \lambda_h \lVert H \rVert _f^2 $$

1. the error functions differ - loss in BPR is smooth and motivated by the MLE.
2. BPR-Opt criterion is generic and can be applied to several models, whereas their method is specific for MF.
3. MMMF is designed to work with sparse explicit data
i.e. they assume that there are many missing values and thus they assume to have much less pairs than in an implicit setting.
—

leave one out (remove one entry from $I_u^+$ per user $u$)

$$ AUC = {1 \over |U|} \sum_u {1 \over |E(u)|} \sum_{(i,j) \in E(u) } \delta( \hat{x}_{ui} > \hat{x}_{uj})$$

where the evaluation pairs per user $u$

$$ E(u) := \{(i,j) | (u,i) \in S_{test} \text{ and } (u,j) \notin (S_{test} \cup S_{train}) \} $$

higher value of AUC indicates a better quality.

—
##### \<Data\> MovieLens100K ( user 943 $\times$ item 1,682, 100K ratings )



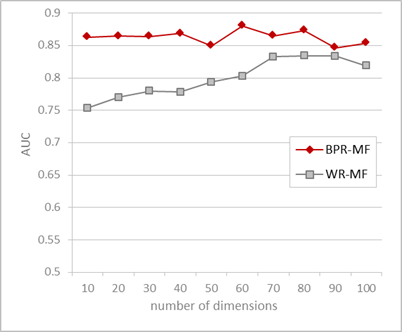
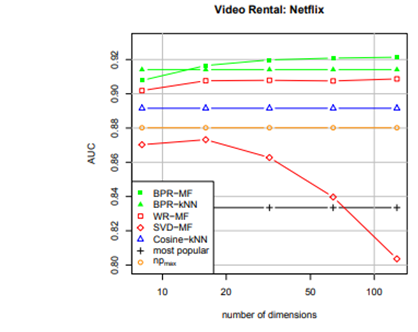
###### remove rating scores, repeated 5 times, $\lambda = 0.0025$, $\alpha = 0.05$
—

# END

#install.packages("rrecsys", force=TRUE, dependencies=TRUE)


test_index<- function(data, na=TRUE) {
  index_test<-c()
  for (i in 1:dim(data)[1]) {
    if(na) indeX_i <- which(!is.na(data[i,]))
    else index_i<-which(data[i,]==0)
    
    index_test[i]<-index_i[sample(1:length(index_i),1)]
  }
  test_index <- index_test
}


train <- function (data, index_test, na=TRUE) {
   
  train_data<-data
  for (i in 1:dim(data)[1]) {
    train_data[i,index_test[i]]<-NA
  }
  train_data[is.na(train_data)]<-0
  train<-train_data
}



calc_AUC <- function(data, pred, index_test, na=TRUE) {
  AUC_u <- 0
  for (i in 1:dim(data)[1]) {
    i=1
    if(na) index_j<-which(is.na(data[i,]))
    else  index_j<-which(data[i,]==0)
    
    AUC_u <- AUC_u + 1/length(index_j) * sum(pred[i,index_test[i]] > pred[i,index_j])
  }  
  
  calc_AUC <- AUC_u / dim(data)[1]
}

############################################
############################################
############################################
############################################
############################################


# check data
which(apply(is.na(data2),1,sum)>1680)

which(apply(is.na(data2),2,sum)<10)
sum(!is.na(data2))




############################################
############################################

ml100k_ori<-ml100k
ml100k[ml100k>0]<-1

index_test<- test_index(ml100k, na=FALSE)
data2_train<-train(ml100k,index_test, na=FALSE)
############################################
############################################

############################################
############################################
####BPR
library("rrecsys")
setwd("C:/Users/heeseoklee/Downloads/rrecsys-master/rrecsys-master/R")
source("ALG_BPR.R")  #BPR2


showDeltaError()
#rrecsys(ratings, alg="BPR")

ratings<-defineData(data2_train)  



AUC_total<-c()
for (i in 1:10) {
  AUC<-0
  for( j in 1:5){
    model_bpr<-BPR2(ratings,k=10*i)
    pred_bpr<-predict(model_bpr)
    
    AUC<-AUC+calc_AUC(ml100k,pred_bpr,index_test,na=FALSE)
  }
  AUC_total[i]<-AUC/5
}
AUC_total_bpr<-AUC_total


setStoppingCriteria(autoConverge = FALSE,
                    deltaErrorThreshold = 1e-05, nrLoops = NULL, minNrLoops = 10)
showStoppingCriteria()



############################################
############################################
####WRMF

#devtools::install_github("dselivanov/reco")
#library("reco")

install.packages("devtools")
####R CMD INSTALL rsparse-master/
devtools::install_github("dselivanov/rsparse", force=TRUE)
library(rsparse)


data("movielens100k")

library(Matrix)
Matrix(movielens100k)

ml100k<-as(movielens100k, "matrix")#[1:10,1:10]

AUC_total<-c()
for (i in 1:10) {
  AUC<-0
  for( j in 1:5){
    fb<-"implicit"
    #fb<-"explicit"
    model = WRMF$new(rank = i*10, lambda = 0.0025,
                     feedback = fb,#c("implicit", "explicit"),
                     init_stdv = 0.01,
                     n_threads = parallel::detectCores(),
                     non_negative = TRUE,
                     solver = "conjugate_gradient",#c("conjugate_gradient", "cholesky"),
                     cg_steps = 5L,
                     components = NULL)
    
    x<-as(data2_train, "CsparseMatrix")
    #x<-movielens100k
    n_users_rank<-model$fit_transform(x, n_iter = 10L)
    rank_n_items<-model$components
    
    pred_mmmf<-n_users_rank %*% rank_n_items
    
    AUC<-AUC+calc_AUC(ml100k,pred_mmmf,index_test,na=FALSE)
  }
  AUC_total[i]<-AUC/5
}

AUC_total_wrmf<-AUC_total







############################################
############################################
####SVD-MF
#install.packages("recommenderlab")
library("recommenderlab")


ml <- as(data2_train,"realRatingMatrix")
r_svd <- Recommender(ml, method = "SVD",param=list(k=10))
p.svd <- predict(r_svd, ml, type = "ratings")


pred_svd<-getModel(r_svd)$svd$u %&% diag((getModel(r_svd)$svd)$d) %*% t(getModel(r_svd)$svd$v)

AUC<-calc_AUC(ml100k,pred_svd,index_test,na=FALSE)




r <- Recommender(data = ml, method = "ALS", 
                 parameter = list(normalize=NULL, lambda=0.0025, n_factors=10, 
                                  n_iterations=10, seed = NULL, verbose = FALSE)) 
r
recom_ratings <- predict(r, newdata = ml, type = "ratings")
as(recom_ratings, "matrix")

getModel(r)




AUC_total<-c()
for (i in 1:10) {
  AUC<-0
  for( j in 1:2){
    fsvd<-funkSVD(ml, k = 10, gamma = 0.0025, lambda = 0.01,
               min_improvement = 1e-06, min_epochs = 30, max_epochs = 50,
               verbose = TRUE)
    
    pred_svdf <- tcrossprod(fsvd$U, fsvd$V)

    AUC<-AUC+calc_AUC(ml100k,pred_svdf,index_test,na=FALSE)
    
  }
  AUC_total[i]<-AUC/2
}

AUC_total_svdf<-AUC_total