인공신경망? 딥러닝? 회의에서 당당하게, 수식없이 알아보자
이전편 보기
랜덤포레스트가 뭐길래? 회의에서 당당하게, 수식없이 알아보자
라쏘? 로지스틱? 회의에서 당당하게, 수식없이 기초개념부터
이번 분류 모형은 3개 층을 가지는 Neural Network 를 사용했습니다.
딥러닝 blah.. 인공지능 blah..
누가 뭐라해도 요즘의 핫한 주제는 인공지능이다. 특히 딥러닝을 통한 이미지, 영상, 자연어처리 등을 통해 다양한 서비스가 나오고 있고, 여러 분야에 적용되고 있다. 그래서 '나도 인공지능이 어떻게 동작하는지 알고 싶다'는 생각을 하고, 인터넷에 검색을 해본다.
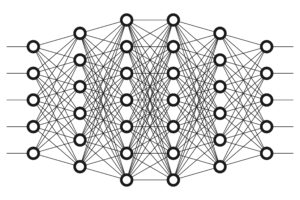 Fig. 1: 이미지출처:[[https://www.datanami.com/2017/05/10/machine-learning-deep-learning-ai-whats-difference/]]
Fig. 1: 이미지출처:[[https://www.datanami.com/2017/05/10/machine-learning-deep-learning-ai-whats-difference/]]
저게 뭐지? 의사결정나무 같은건가? 엄청 복잡하네.. 라고 생각을 하고는 생각을 접게 되는 경우가 대다수이다.
조금 어렵게 느껴질 수도 있겠지만, 이번 기회에 기본적으로 인공신경망, 딥러닝이 어떤 방식으로 동작하는지 알아보는 시간을 가져보자.
- 인공지능과 딥러닝의 차이
- 인공신경망과 딥러닝
- 계산방법 (경사하강법, 오차역전파)
순으로 알아보도록 하겠다.
인공지능, 머신러닝, 딥러닝
많이들 들어본 얘기겠지만, 아직 용어에 대한 혼동이 많은 사람들을 위해서 인공지능과 머신러닝, 딥러닝, 인공신경망 등 이러한 용어들에 대한 얘기부터 하고 넘어가야 겠다.
한마디로 쉽게 얘기하면,
인공지능 $ \supset $ 머신러닝 $ \supset $ 인공신경망 $ \supseteq $ 딥러닝
이다.
인공지능은 '인간의 지능을 인공적으로 모사하는 것'을 의미하는 가장 큰 의미라고 생각할 수 있다.
이러한 방법 중 크게 '규칙 기반'으로 사전에 규칙을 정해서 판단,추론을 하는 방법과 데이터를 통해서 모형을 학습하게 하는 '머신러닝(기계학습)' 분야가 있다고 생각할 수 있다. 규칙기반은 인간이 미리 정해둔 규칙 ( if A then B ) 를 통해서 판단을 하는 것이고, 기계학습은 데이터를 학습 모형/알고리즘에 집어넣어서 그런 규칙들을 자동으로 찾을 수 있게 만드는 방법이다.
인공신경망이나 딥러닝은 '머신러닝'의 여러가지 기법 중의 하나로서, 이전편들에서 보았던 의사결정나무, 랜덤포레스트, (로지스틱)회귀 등 여러가지 방법들과 같은 레벨에 속한다고 생각하면 되겠다.
그렇다면, 인공신경망과 딥러닝은 무엇이고, 무엇이 다른 것일까? 이제부터 알아보도록 하자.
인공신경망
고등학교 생물시간으로 돌아가 보자. 우리의 몸 안에서 '정보'라는 것을 전달하는 것을 신경세포(뉴런Neuron) 이라고 했던 것 같다. 이런 신경세포가 몸 안에 엄청나게 많이 있고, 이들은 아래와 같은 모양으로 전기적, 화학적 신호를 통해 감각기관에서 뇌까지 정보를 전달한다고 한다.
 Fig. 1: 출처: 위키백과 (https://ko.wikipedia.org/wiki/신경_세포)
Fig. 1: 출처: 위키백과 (https://ko.wikipedia.org/wiki/신경_세포)
수상돌기, 축삭돌기.. 가물가물하지만 어디서 들어본 것 같은 용어들이 나온다. 수상돌기를 통해서 정보를 전달 받고, 역치(임계점) 이상의 자극이 오면 축삭돌기들을 거쳐 말단을 통해서 다른 신경세포로 정보를 전달하는 과정을 통해서 정보가 흘러간다.
이런 신경세포의 정보전달 과정을 흉내내어 만드는 머신러닝 방법이 인공신경망 모형이다.
퍼셉트론
하나의 신경세포 모양을 보자. 아래와 같이 입력값(데이터, 특성)을 받아서, 회귀분석 모형(자극을 만드는 모형)으로 해석한 다음, 역치 이상의 자극(threshold)이 면 +1 을, 아니면 0을 반환하는 모양이 된다. 이런 모형을 '퍼셉트론perceptron' 이라고 한다.
여기서 자극이 역치를 넘는지를 판단하는 함수를 '활성화Activation 함수' 라고 하는데, 쉽게 생각해서 이전시간에 배운 회귀분석 에, 추정값을 어떤 기준으로 1을 반환할지 0을 반환할지를 껍데기로 씌운 것이라고 이해하면 되겠다. 보통은 활성함수로 저렇게 생긴 계단step함수 보다 미분이 가능한 로지스틱/시그모이드 함수, tanh, ReLU 함수 등이 사용된다.
입력값*비중 (-활성함수→) → 1 or 0
인간의 신경세포와 비슷하다고 생각이 되는가?
회귀분석이다
지난 편의 회귀분석 문제를 다시 상기해서 보면, (몸무게, 키, 성별)의 데이터를 가지고 있을 때 몸무게가 60kg이 넘을지 안넘을지를 예측하기 위해서,
- '몸무게 = 키*비중 + 성별*비중' 의 단순 회귀분석을 사용해서 60 이상인지 아닌지 추정하는 방법
- 'log(확률/(1-확률)) = 키*비중 + 성별*비중' 의 로지스틱 회귀를 이용해서 확률로 추정하는 방법
을 이용했다.
퍼셉트론의 경우에 대어보면, 활성함수를 위에서 살펴본 계단step함수를 사용하면 1)번, 로지스틱logistic/시그모이드sigmoid함수를 사용하면 2)번과 완전히 같다. 통계학에서 출발한 학문과 컴퓨터 공학에서 출발한 학문의 만나는 지점이라고 생각해도 좋을 것 같다.
사실 하나의 퍼셉트론만 보면, 회귀분석이나 다른 방법과 비교해서 별로 다른 것도 모르겠고, 이점도 없어 보인다. 실제로는 이 퍼셉트론이 여러개 모이면 파워풀한 결과를 낼 수 있게 된다.
XOR 문제?
먼저 다들 말하는 XOR 문제가 뭔지부터 알아보자.
먼저 AND, NAND, OR 문제는 아래와 같이 쉽게 생각할 수 있다. AND는 둘다 TRUE일때(엑셀에서 AND함수), NAND는 둘다 FALSE일때(NOT(AND)), OR은 둘 중 하나라도 TRUE일 때(OR) 이다. 세상의 많은 문제들을 일반화 시켜보면 이런 모양을 가질 것이다.
TRUE를 1, FALSE를 0으로 놓고 그래프를 그려보면 오른쪽과 같고, 옆에 있는 비중들과 기준값으로 퍼셉트론을 이용해서 TRUE, FALSE를 판별할 수 있다.
직선으로 구분이이 가능한 것에 주목하자.
그런데, 아래와 같은 XOR 문제 (둘 중 단 하나만 TRUE일 때만 TRUE, 배타적논리합이라고 한다) 같은 경우는, 하나의 퍼셉트론(직선)으로는 해결이 불가능하다. 그렇다면 어떻게 하면 좋을까?
위의 그래프를 보면서 잘생각해 보면, NAND와 OR 분류기를 잘 조합하면 될 것 같다. 그래서 아래의 오른쪽과 같이 NAND, OR의 결과물을 AND 분류기로 판별하면 해결이 가능하다.
한 개의 OR, NAND 층을 더함으로써, XOR 같은 문제를 풀 수 있게 되는 것이다.
회귀분석으로 생각해 보면, 선형이 아닌 비선형 문제를 풀기 위해 여러 개의 회귀를 조합하여 비선형의 모양을 만들어 주는 것이다.
인공신경망
이렇게 기본적인 회귀분석 등의 간다한 선형의 모형으로 풀기 힘든 비선형의 복잡한 문제들을 풀기 위해, 여러 개의 퍼셉트론을 모아서 모형을 구성한 것을 인공신경망Artificial Neural Network 라고 한다. 신경세포를 본뜬 퍼셉트론을 여러개 모았으니, 신경망이라고 부르는 것이다.
이런 모양을 층Layer 또는 단계의 모양으로 그림으로 많이 표현하고 있다. 우리가 가지고 있는 데이터인 입력값들이 위치하는 층을 입력층input layer, 예측값이 도출되는 마지막 층을 출력층output layer 이라고 하고, 그 중간에 있는 층들을 은닉층hidden layer이라고 부른다. 몇 개의 층을 입력값과 출력값 사이에 넣을 것인지, 각 층은 몇 개의 퍼셉트론으로 구성할 것인지에 따라 정말 복잡한 문제도 풀 수 있게 된다. 실제로 충분히 많은 숨은 층을 가지고 있으면 대부분의 모양들을 근사할 수 있다고 한다.
서두에서 본 그림과 같이 복잡하게 얽힌 인공신경망의 그림을 보고 '의사결정나무' 같은 것이라고 생각하는 사람들이 있다. 사실은 위에서 처럼 각 퍼셉트론의 출력값들이 다른 층의 퍼셉트론의 입력값이 되고, 또 다음 퍼셉트론으로 전달되는 복잡하게 얽히는 신경계를 모방한 모양이다.
복잡한 그림을 찬찬히 살펴보자.
이렇게 비중 5,6 을 이용해서 중간값3까지 만든다.
중간값1,2,3 은 하나의 은닉층을 통해서 도출된 새로운 입력값으로, 추정값을 만들기 위해서 또 다시 비중들로 계산이 된다.

딥러닝
그렇다면 인공신경망과 딥러닝의 차이는 무엇일까?
딥러닝은 인공신경망을 다르게 부르는 이름으로, 퍼셉트론을 수십, 수백, 수천 층으로 쌓아서 희박한 데이터를 가지는 복잡한 문제(이미지,텍스트,영상 등)를 풀 수 있도록 하는 방법이고, 보통의 회귀/분류 문제에서는 3~4개 정도의 몇 개 안되는 숨은 층을 사용한다.
인공신경망은 1) 계산이 복잡하고, 2) 느리고, 3) 과적합Overfitting 이 생길 가능성이 높아서 한동안 인기를 못 끌다가, 2006년에 캐나다 토론토대학의 제프리 힌튼 교수에 의해 딥러닝이라는 말로 다시 태어났다. 과적합 방법을 다른 방법을 통해서 해결하였는데, 기존의 인공신경망이라는 단어가 가지는 부정적인 인상을 없애기 위해서 만들었다는 이야기가 있다. 물론 GPU 등 컴퓨터 계산 성능의 발달도 큰 역할을 했다.
블랙박스?
딥러닝은 블랙박스라는 얘기를 많이 하는데, 그냥 계층이 두 개인 아래의 경우만 살펴보자.
결과추정값
= 비중*중간
= 비중*(중간1*비중+중간2*비중)
= 비중* ( (입력1*비중+입력2*비중)*비중 + (입력1*비중+입력2*비중)*비중)
위와 같이 계층이 두개만 되어도 입력 값들이 어떻게 추정값에 영향을 미치는지, 결과 식이 복잡해져 해석하기가 상당히 곤란해진다. 수십, 수백개의 층이 존재하고 입력값이 수천, 수백만개가 되면 정말 어렵다. 이래서 딥러닝 모형을 블랙박스Black Box라고 한다.
요즘은 입력값을 조금씩 변화시키면서 결과값이 변하는 추이를 보면서 변수의 중요도를 계산하는 등 설명 가능성을 높이기 위한 노력이 행해지고 있다는 것도 알고 있으면 좋을 것이다.
지난 편 내용을 통해서 간단한 회귀모형을 알고 있으면 딥러닝이라는 것이 복잡하게 보이기는 하지만, 사실 회귀분석을 여러 개/층을 쌓은 것과 같은 의미라고 생각하면 크게 어렵지 않은 것을 확인할 수 있다.
위에서 살펴보았듯이 고려해야 할 점이 있다면, 계산을 어떻게 해서 복잡한 수식의 비중(계수)들을 빠르게 찾을 수 있을 것인가일 것이다. 그럼, 이 복잡한 모형에서 비중(계수)들은 어떻게 추정할까?
학습=비중 찾기
이전편 에서 오차 함수를 최소로 하는 계수들을 찾는 것이 목적이라고 했던 것을 기억하자. 퍼셉트론이나 딥러닝이나 모두 같은 방식이다. 다만, 여기서는 복잡한 미분 값을 계산하기가 힘들기 때문에 컴퓨터로 가까운 값을 추정하는 계산을 한다는 점이 조금 다를 뿐이다.
오차(목적)함수에 대해서 다시 한번 간단히 떠올려보자. 우리가 (몸무게, 키, 성별)의 데이터 쌍을 가지고 있고,
몸무게 = 키*비중1 + 성별*비중2
의 모형으로 몸무게를 예측하고자 했다.
여기서 비중1,2를 찾는 것이 우리의 문제이고, 목적은 몸무게를 잘 예측하는 것이다. 즉,
오차 = (데이터의 몸무게 - 모형으로 추정한 몸무게)
= (데이터의 몸무게 - (키*비중+성별*비중))
를 가장 작게 하는 비중의 값을 찾고자 하는 것이다.
미분이란
지난 시간에 보통 오차함수의 미분을 통해서 최소값을 찾는다고 언급한 적이 있다. 그렇다면 미분에 대해서 잠깐 살펴보고 넘어가도록 하자. 미분이란 뭘까? 쉽게 설명하자면,
미분 = 변화율 = 기울기
= 값이 아주 조금 변화했을 때 함수 값이 변하는 정도
그렇다면 오차의 미분이란, 비중이 조금 변했을 때 오차 값이 얼마나 변하는지를 알아보는 것이다.
경사하강법
미분을 이용해서 오차의 최소값을 찾는 방법 중 하나를 살펴보자. 경사하강법이라는 것으로 딥러닝에서 가장 많이 사용하는 방법이다.
데이터는 (몸무게, 키) = (60, 170) 하나 밖에 없다고 하고, '몸무게 = 키*비중' 모형으로 오차를 최소화 하는 비중을 찾아보자. 오차 함수는 (몸무게-(키*비중))2이다.(실제는 보통 제곱으로 오차함수를 구성한다). 데이터가 하나이니까 계산기로 두드려보면, 당연히 오차를 최소로 하는 비중은 60/170= 0.35 일 것이다.
데이터가 많아지고, 찾고자 하는 비중들이 많아지면 단순한 계산으로는 최소값을 찾기 힘들다. 그 때 아래의 경사하강법을 이용해서 오차의 최소값을 구할 수 있다.
경사하강법Gradient Descent Method 이란 함수의 최소값을 찾기 위해서 경사(미분)을 이용해서 값을 업데이트 하는 방법이다. 많은 곳에서 '산을 내려가는' 것으로 비유하여 설명하고 있는데, 간단하게 알아보자.
0. 하산문제: 산의 고도가 낮은 곳으로 내려가야 한다.
경사하강: 오차함수 값이 작은 값(비중)을 찾아야 한다.
함수와 그래프에 대해서 익숙하지 않은 사람들을 위해서, 잠시 생각해보자.
비중이 어떤 값을 가질 때마다 오차도 어떤 값을 가질 것이다. 위의 오차함수에서 비중이 0일 때, 오차는 (60-0)2 = 3,600 일 것이고, 1이면 (60-170)2=12,100, 0.35일 때 0으로 최소일 것이다. 이런 점들을 모아서 그래프로 표현해보면 아래와 같다.

이런 그래프를 산의 한 모습이라고 생각해 보면, 어떤 비중 값에 대한 오차값을 최소화하는 것과 산을 내려가는 것의 유사점을 찾을 수 있을 것이다.

1. 하산문제: 현재 위치, 산의 중턱 어느곳에 있다.
경사하강: 찾고자 하는 비중 값을, 무작위로 아무 숫자나 골라보자. 예를 들어 0.1 이라고 지정하자.
2. 하산문제: 일단 여기가 어딘지를 봐야 하니까 고도계를 보자.
경사하강: 오차값을 계산해보자. 오차는 (60 - (170*0.1))2 = (60-17)2 = 432 이다.
3. 하산문제 : 어느쪽이 내려가는 방향인지 찾아보자.
경사하강: 어느쪽이 내려가는 방향인지 찾아보자.
아래 그림에서, 지금이야 이렇게 그래프의 모양을 보면서 당연히 오른쪽으로 가야된다고 생각할 수 있지만, 데이터값이 늘어나고 찾아야 하는 변수들의 숫자들이 많아지면 그림을 그려서 볼 수가 없다. 어느 방향으로 가야할지 조차 미궁에 빠지게 된다.

이 때 미분값(기울기)의 방향이 값이 커지는 방향이라는 것을 아래 그래프를 통해 확인해보면, 기울기의 반대방향으로 가면 값이 작아지는 방향으로 간다는 것을 알 수 있다.(기울기가 음(-)인데, 음의 방향으로 가면 오차 값이 커진다)
4. 하산문제 : 가장 가파르게 내려가는 곳으로 한 발짝 움직이자.
경사하강: 비중 값을 기울기(미분값)로 업데이트 하자.
물론 산에서 가장 가파르게 내려간다고 절벽으로 발걸음을 내딛지는 않겠지만, 최소값을 찾기 위해 컴퓨터는 절벽으로 내려가는 것이 가장 빠르고 좋은 방법이다.
산에서는 내 눈과 발의 감각으로 가파른 곳을 알 수 있다. 함수에서는 미분값, 즉 기울기Gradient 가 가장 '가파르게' 내려가는 방향이다. 그래서 경사Gradient하강Descent 방법이다. (참고_calculus) 미분을 배워본 사람은 쉽게 찾을 수 있다. 기울기 = -2(몸무게-(키*비중)) = -2(60-17) = -86
한발짝 움직이는 것은 원래 비중값 (0.1) 에 기울기의 반대방향으로 값을 더해주면 된다.
비중 - (보폭)*(기울기)
= 0.1 - (보폭)*(-86)
여기서 보폭 값은 사람마다 보폭이 다르듯이 우리가 정해주어야 한다. 0.001 로 해보자.
= 0.1 - 0.001*(-86) = 0.1+0.086 = 0.186
5. 하산문제 : 한발짝 움직였으니, 얼마나 내려왔나 고도계를 다시보자.
경사하강: 비중 값을 업데이트 했으니, 오차값을 다시 계산해보자. (계산 편의를 위해 0.186=0.2로 계산)
오차 = (60-170*(0.0186))2 = 262
실제로 오차값이 줄었다!
6. 하산문제: 3~5번을 반복하자. 더이상 내려갈 곳이 없을 때까지
경사하강: 3-5번을 반복하자. 더이상 내려갈 곳이 없을 때까지
보폭을 잘 정해주면, 최소값으로 수렴할 것이다.
실제로는 이 방법은 보폭의 크기나 시작하는 위치에 따라서, 모든 함수값에서 '최소값'이 아닌 근처에서의 '최소값'을 가질 수도 있긴 하다.

이런 문제 때문에, 초기의 무작위 값을 바꿔가면서 학습하기도 하는 방법을 사용하기도 하고, 보폭 자체도 조절 변수로 찾기도 한다. 그런데 사실 숨은 층의 개수가 많고 복잡하면 국소적인 최소값으로도 어느정도 성능을 보장하기 때문에 넘어가는 경우도 있다.
이렇게 미분과 경사하강법을 사용하면 비중들의 값을 찾을 수 있다.
그런데, 여러 층들이 얽혀있는 딥러닝에서는 미분값을 계산하는 것 자체가 문제가 된다. 상당히 오랜 시간이 걸린다. 퍼셉트론이나 퍼셉트론을 층으로 쌓는 방법들이 나온지는 오래된 이론이지만 컴퓨터 성능이 받쳐주지 못했기 때문에 늦게 유명해진 것이다. 컴퓨터 성능의 비약적인 발전과 더불어 또 계산 속도를 빠르게 할 수 있는 방법이 소개되었는데, 오차역전파법(back-propagation of error) 이다.
오차역전파법
여러 층을 가지는 신경망에서 오차역전파를 이용하면 미분값 계산을 비교적 빠르게 할 수 있다.
층마다 퍼셉트론이 하나씩만 있는 신경망을 생각해보자. 우리가 학습을 할 때, 입력(데이터)를 통해서 여러 비중값의 계산을 하고, 층들을 거쳐서 추정값을 낸다.

오차 역전파는, 이렇게 나온 오차들을 역으로 입력값 쪽으로 전파하여 비중들의 미분값을 계산하는 방법이다.

내가 처음봤을 때와 동일하게, 그림만 봐서는 당연히 무슨 말인지 모를 것이라고 생각한다. 그래서 조금이라도 자세하게 설명을 해 보자.
미분값 계산의 어려움
먼저, 위에서 설명한 미분에 대해서 다시 살펴보자.
미분 = 비중의 값이 아주 조금 바뀌었을 때, 오차의 변화량
오차함수를 풀어 써보자.
오차함수
= (실제값 - 추정값)2
= (실제값 - ( 중간값 *비중2) )2
= (실제값 - ( (입력값*비중1)*비중2 ) )2
이다.
이 오차함수의 미분값을 찾아야 하는데, 고등학교 때 배운 함수 수식을 계산하는 방법과 미분의 정의를 이용한 방법이 있다.
함수수식을 이용한Closed Form 미분값 찾기
$ X^2 $ 을 미분하면 2X
가 되는 것 처럼 수식을 이용해서 함수꼴을 찾을 다음 계산하는 방법이 있다. 위에서는 각 층마다 1개씩의 퍼셉트론 밖에 없고 퍼셉트론에도 찾아야 할 비중값이 1개 밖에 없어 충분히 가능해 보이지만, 비중과 층의 수가 늘어나면 풀기쉬운 함수 모양으로 미분을 정리해서 계산하는 것은 불가능에 가깝게 된다.
미분의 정의 이용
그래서 신경망에서는 미분의 정의를 이용해서 미분값을 구해야 한다. 아주 작은값을 이용해서
(실제값 - (입력값*(비중1+아주작은값)*비중2) )2 - (실제값-(입력값*(비중1))*비중2)2
가 수렴하는 지점까지 계산해 주어야 한다.
그런데 비중의 변화에 대한 오차값의 변화를 직접 계산하기 위해서는, 앞으로 전달되는 값들을 계속 계산 해주어야 한다.(비중1이 바뀌면 중간값이 바뀌고, 중간값이 바뀌면 예측값이 바뀐다) 즉, 비중의 개수가 늘어나면 그 개수의 제곱에 비례하는 계산이 필요하다. 계수들이 늘어날 수록 계산이 엄청나게 많아진다.
대신, 오차역전파법에서는 미분의 연쇄법칙Chain Rule 을 이용해서, 선형적인 계산속도로 연산을 수행할 수 있도록 한다.
연쇄법칙(체인룰Chain rule)
연쇄법칙(체인룰)이란
합성함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.
는 의미다.
합성함수부터 무슨 말인지 모르겠다.
비중1→회귀식→중간값
에서 중간값을 내는 활성함수의 입력값으로 회귀식이 들어가게 되는데, 회귀식은 또 입력값과 비중의 함수로 이루어져 있다. 이렇게 함수 내에 함수가 또 들어간 함수를 합성함수라고 한다.
연쇄법칙이란 이런 합성함수(중간값)를 비중으로 미분한다고 했을 때
중간값의 비중에 대한 미분
= 중간값의 회귀식1에 대한 미분
x 회귀식1의 비중에 대한 미분
같은 방식으로 계산할 수 있다는 뜻이다.
연쇄법칙은 미분(기울기)을 분수 꼴로 표현해서 보면 더 쉽다.

$ \Delta $ 는 변화량을 의미하고, 따라서 왼쪽 항의 경우 비중의 변화량에 대한 중간값의 변화량이니까 기울기, 즉 미분 값이 된다.
그럼 이제 이 연쇄법칙을 통해서 어떻게 계산을 빠르게 할 수 있는지 알아보도록 하자.
비중2의 계산
위 그림에서 비중2가 오차에 미치는 영향, 미분값을 구해보자.

체인룰에 의해서 비중2와 오차 사이에 존재하는 회귀식2, 추정값으로 미분을 분해해서 총 3가지 값의 곱으로 표현이 된다.
그림을 자세히 보면,
① 비중→회귀식2 : 중간값을 그대로 적용
② 회귀식2→추정값 : 활성함수의 미분 (수식으로 계산이 가능하다)
③ 추정값→오차 : 오차함수의 미분 (수식으로 계산이 가능하다)
로, 세 개 값을 곱하면 미분값을 구할 수 있다. (②와 ③은 간단한 수식이라서 수식으로 미분값을 바로 계산할 수 있다)
여기는 말단이니까, 크게 계산의 이점은 없어 보인다. 하지만 비중1을 계산할 때를 보자.
비중1의 계산
① 비중1→회귀식1 : 입력값을 그대로 적용
② 회귀식1→중간값 : 활성함수의 미분
③ 중간값→회귀식2 : 비중2의 값을 그대로 적용
④ 회귀식2→ .. → 오차 : 이 부분은 앞서 비중2 미분을 계산할 때 사용한 값을 쓰면 된다.
로, 네 개 값을 곱하면 미분값을 구할 수 있다. 역시 간단한 수식들의 미분과 앞서 구한 값들을 이용한다는 것을 확인해보자.
언뜻보면 복잡해 보이지만, (실제로 복잡하긴 하다..) 여기서 중요한 점은, 활성함수의 미분이나 오차함수의 미분 등이 모두 정해진 모양으로 값만 입력하면 된다는 것이다. 따라서 기초적으로 미분값을 계산하는 것보다 비교적 간단한 연산(국소적 연산)만으로 미분값을 구할 수 있기 때문에 계산 속도가 훨씬 줄어들어, 제곱에 비례하는 것이 아닌 선형적으로 비례하는 계산 시간을 갖게 된다.
학습에 사용되는 용어들
인공신경망을 학습하는 데 사용되는 테크닉에 관련된 몇가지 용어들이 있다. 회의에서 들어볼 것 같은 용어들에 대해서 한 번 살펴보자.
- 학습률Learning rate : 경사하강법에서 살펴본 '발자국'의 크기이다. 학습이 진행되면서 바뀌는 방법도 있다.
- 미니배치mini-batch : 오차를 구하려면 모든 데이터에 대해서 실제값과 예측 값의 차이를 계산해 주어야 한다. 하지만 딥러닝에서는 데이터의 양이 엄청 많기 때문에 이 것도 부담이 된다. 그래서 데이터의 일부분만을 사용해서(무작위로 추출) 오차의 '근사값'을 통해서 학습을 하게 되는데, 이런 것을 미니배치라고 한다.
데이터를 무작위로 추출해서 학습한다는 의미로 확률적stochastic 경사하강법 이라고도 한다.
- 에포크epoch : 미니배치 학습에서 훈련 데이터를 모두 소진했을 경우 1에포크라고 한다.
예를 들어 10000개의 학습 데이터로 100개 단위의 미니배치를 수행하면, 100번 미니배치가 실행되면 1에포크가 되는 것이다.
- 드롭아웃drop-out : 딥러닝을 하게 되면 큰 문제가 과적합overfitting 이 생기는 것이다. 이를 방지하기 위해 추정해야 하는 비중들 중 일정비율을 값을 0으로 만들어 의도적으로 과적합을 방지하기도 한다.
마무리
지금까지, 어렵지만, 인공신경망, 딥러닝의 기본에 대해서 알아보았다.
1) 퍼셉트론이란 인간의 신경세포를 본 떠 만든 모형으로 회귀분석과 같은 말이다.
2) 퍼셉트론 하나만으로는 비선형 문제를 풀 수 없어서 여러개를 겹쳐서 사용하는데, 이 것을 인공신경망이라고 한다.
3) 여러 층을 가진 인공신경망을 학습하기 위해, 오차를 최소화하는 데 경사하강법을 사용한다.
4) 경사하강법은 오차를 미분하여 미분값의 방향으로 한 발짝식 움직이면서 최소값을 찾아가는 방법이다.
5) 여러 층을 가지는 인공신경망에서는 미분값을 빠르게 계산하기 위해 오차역전파법을 사용한다.
6) 오차역전파법은 합성함수 미분의 연쇄법칙을 이용해서, 제곱에 비례하는 계산 시간을 선형적인 계산시간으로 줄여준다.
기본적인 딥러닝은 이렇게 이루어진다. 물론 과적합을 막기 위한 여러 방법들과 CNN, RNN, 강화학습 등 많은 변형들이 있지만 기본적으로는 동일한 매커니즘으로 이루어진다. 아직 많이 연구되고 있는 핫한 분야이기도 하고, 많은 변형들과 테크닉들이 포함되어 있기 때문에 단순히 이번 설명으로는 딥러닝에 대해서 모두 설명할 수는 없을 것이다.
딥러닝이 많은 문제를 잘 푸는 것으로 알려지고 있지만, 딥러닝의 가장 큰 문제점은 복잡함으로 인해 생기는 '과적합'과 '학습시간', '컴퓨터 성능 비용', '전기 이용 비용' 등이다.
염두해 두어야 할 것은, 딥러닝이 아주 큰 인기를 끌고 있고 현재의 많은 혁신적인 서비스들이 딥러닝 기반의 인공지능을 기반으로 하고 있지만 자연어처리나 이미지 인식 등의 복잡한 문제가 아닌이상 보통의 머신러닝 문제에서는 시간과 비용의 문제 등으로 다른 간단한 방법을 더 많이 사용한다는 것이다.
많은 단점들이 개선되고 있고, 언젠가 해결될지도 모르겠지만, 기본적으로 모든 문제에 무조건 좋은 모형은 없기 때문에 무조건 딥러닝을 요구하기 보다는 항상 trade-off를 고민하여 문제를 풀려고 해야 할 것이다.
마지막으로 KDnuggets 에 올라온 데이터 사이언스에 대한 불편한 진실에 있는 말을 염두해 볼 필요가 있겠다 1)
95%의 일에는 딥러닝이 필요하지 않다
실제 분석의 90%는 일반화 선형모델(GLM)으로 해결된다.
Reference
Pattern Recognition and Machine Learning, Christopher M. Bishop, SPRINGER, 2007
Computer Age Statistical Inference, Bradley Efron 外, Cambridge University Press, 2016
The Elements of Statistical Learning, Trevor Hastie 外, Springer, 2001
밑바닥부터 시작하는 딥러닝(Deep Learning from Scratch), 사이토 고키, 개앞맵시 역, 한빛미디어, 2017
골빈해커의 3분 딥러닝, 김진중, 한빛미디어, 2017
More
| 2021/09/24 06:30 | |
| 2020/06/18 11:34 | |
| 2020/06/07 14:03 | |
| 2020/05/28 10:29 | |
| 2020/05/12 09:03 | |
| 2020/05/07 09:27 | |
| 2020/04/29 10:52 | |
| 2020/04/20 11:12 | |
| 2020/04/16 15:23 | |
| 2020/04/15 07:21 | |
| 2020/04/11 01:41 | |
| 2020/04/08 06:49 | |
| 2020/04/01 00:55 | |
| 2020/03/21 13:43 | |
| 2020/03/20 11:53 | |
| 2020/03/15 11:11 | |
| 2020/03/07 07:35 | |
| 2020/03/01 16:09 | |
| 2020/02/29 04:52 | |
| 2020/02/29 04:52 | |
| 2020/02/29 04:52 | |
| 2020/02/29 04:52 | |
| 2020/02/29 04:52 | |
| 2020/02/29 04:49 | |
| 2020/02/06 12:58 |







Discussion