기획,분석가가 알아야 할 사람에 대한 사실:무작위편향
기획, 분석가를 위한 사람에 대한 사실 : 목록
| 2020/06/07 14:03 | |
| 2020/05/28 10:29 | |
| 2020/05/07 09:27 |
애플의 아이팟ipod 이라는 MP3 재생 기기를 기억하는가? 아이폰Iphone 등장 이전 음악 재생의 습관을 바꿔놓았던 이 기기를 사용하던 고객들은, 불량품을 받았다고 생각하는 경우가 많았다고 한다.
바로 '셔플Shuffle' 이라는 랜덤 재생 기능을 사용할 때, 같은 노래들이 두번 연속 들리는 등 '무작위'가 아니라는 느낌이 들었기 때문이다.
그에 답해서 2005년의 Keynote에서 스티브잡스가 이렇게 말했다.
 Fig. 1: 출처:구글이미지, https://www.youtube.com/watch?v=7GRv-kv5XEg
Fig. 1: 출처:구글이미지, https://www.youtube.com/watch?v=7GRv-kv5XEg
재생 목록이 10개라면, 정말 무작위로 복원추출을 한다면, 한 노래 다음에 같은 노래가 또 나올 확률은 1/10이다. 10번 중 1번은 그런 일이 충분히 생길 수 있게 된다.
이렇듯 사람들은 무작위random 에 대해서 잘 인지 하지 못한다.
생일 문제, 역설 (birthday paradox)
임의의 두 사람이 생일이 같을 확률은 얼마일까? 365일 중 하루가 생일일 것이므로 1/365 * 1/365 로 약 1/13만 의 확률이다.
하지만, 30명 한 반에서 어떤 두 사람이 생일이 같을 확률은? 70%가 넘는다!!!
계산은
(1-모두 다를 확률= 1- 364/365*363/365*…)
로 계산한다. 자세한 것은 링크 를 확인해보자.
링크를 보면 알겠지만, 60명만 넘어가면 99%가 넘어가서 거의 무조건 생일이 같은 사람이 있다.
무언가 패턴이 있어 보이는가? 하지만 무작위로 충분히 일어날 수 있는 일이다.
비슷한 예로, 1985년 미국에서 4개월 만에 복권에 두 번 당첨된 사람이 있다고 한다. 해당 확률은 17조 분의 1이라고 한다. 분명 억세게 운이 좋은 사람인 것만은 확실하다.
하지만 복권이 조작되었다느니 저 사람에게 무언가가 있지 않나하는 음모론은 접어두자. 한 특정 사람이 복권에 당첨될 확률은 엄청나게 작지만, 미국인 3억명 중 누군가가 그런 행운이 생길 확률은 생각보다 높기 때문이다.
하버드 대학의 퍼시 디아코니스Percy Diaconis와 프레더릭 모스텔러Frederick Mosteller가 계산한 바로는 미국의 어떤 누군가에게 그런 일이 발생할 확률은 1/30 으로 생각보다 엄청나게 높은 확률이라고 한다.3)
내가 아닌 '무작위의 사람'을 생각하면 생각보다 자주일어난다. 항상 무엇인가 있어 보이는 사건도 생각보다 자주 일어날 수 있다는 사실을 잊지 말자. 특별하게 받아들여야 하는 사건인지 신중히 고민해봐야 할 것이다.
여담으로 두번 복권 당첨된 행운의 주인공은 도박에 당첨금을 다 탕진했다고 하니 너무 부러워 하지는 말자.. 4)
내가 생각하는 무작위가 무작위일까?
무작위로 100개의 점을 찍으면 각 칸에 1개씩 들어갈까?
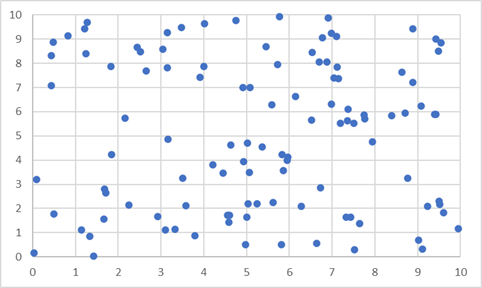
빈 칸들이 많이 보이지 않은가? 자세히 바라보면 어떤 패턴을 찾을 수도 있겠다. 뭔가 무리를 지어서 보이지 않는가? (0,8)에서 (10,0) 으로 이어지는 선으로 두 무리가 나눠져서 보이는 것도 같다.
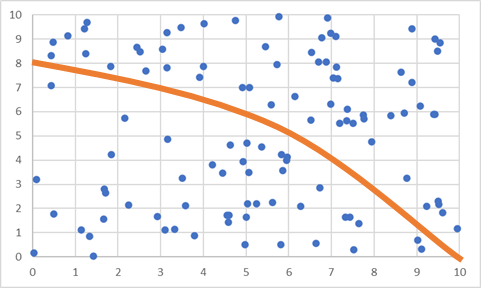
실제는 무작위로 분포한 점이지만, 우리 눈은 어떤 패턴을 찾으려는 경향이 있다.
비슷하게 별의 광원의 예시를 들 수 있다. 우리가 하늘에 보이는 별은 무작위로 볼 수 있지만, 우리 눈으로 보기에는 무리 짓는 성질이 있다. 우리 눈은 무작위에서도 패턴을 찾고자 하기 때문이다. 그래서 별자리 같은게 생기지 않았을까?
듬성듬성 분포하는 게 꼭 무작위인 것은 아님에 주의해야 한다.
실제 데이터에 비임의성이 전혀 없으면, 인위적일 가능성이 존재한다.
반대로 생각해 보면 무작위 데이터에는 항상 어떤 패턴이 존재하기 때문에 이미 벌어진 사건에 대해서 함부로 해석하는 것도 경계해야 한다. 뉴스에서 많이 보는 성공 사례들도 사실은 운 때문일 가능성이 많지만 항상 언론과 대중들은 이유를 찾아낸다. 이를 사후검증 오류라고 한다.
벤포드의 법칙
실세계에서 존재하는 많은 수치 데이터의 10진법 값에서 수의 첫째 자리의 확률 분포를 관찰한 결과, 첫째 자리 숫자가 작을 확률이 크다는 법칙이다. 벤포드의 법칙을 따르는 데이터 집합에 등장하는 수들의 첫째 자리가 1일 확률은 약 30%인 데 반해, 9가 첫째 자리로 등장할 확률은 5% 정도밖에 되지 않는다. 5)
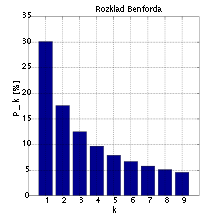 Fig. 1: 출처:wikipedia-Benford's_law
Fig. 1: 출처:wikipedia-Benford's_law
전기요금 고지서, 도로명 주소, 주식 가격, 주택 가격, 인구수, 사망률, 강의 길이, 물리 상수와 수학 상수 등 다양한 데이터에 등장하는 수들이 벤포드의 법칙을 따른다고 한다. 6)
무작위로 분포할 것 같은 많은 숫자들에서 이러한 법칙이 성립한다는 것은 우리가 생각하는 '무작위'가 실제와 얼마나 다른지를 보여주는 한 가지 예시가 될 수 있다.
보통 사람들이 수치를 조작할 때, 1-9 를 균일하게 분포하도록 조작하는 경향이 있다고 한다. 따라서 실제로 미국 국세청 등 많은 기관에서 이 법칙을 응용하여 회계 부정을 탐지하는 데 사용한다고 한다. 그 외에도 많은 숫자 조작을 밝혀내는 데 이용되고 있다.
속지말자. 정말 균일하면 의심해보자.
생각해볼 점
진짜 자연스러운 것과 사람들이 생각하는 자연스러움은 다를 수 있다.
1) random은 random 이다. 쓸데없이 패턴을 찾으려고 하지 말자.
2) 나를 중심으로 하는 것에서 벗어나서 크게 보자. 안일어날 것 같은 사건도 생각보다 확률이 높다. 괜한 음모론 만들지 말자.
3) 무작위와 균일한 분포는 동치가 아니다.
Reference
틀리지 않는 법,조던 엘렌버그 저, 열린책들, 2016
행운에 속지 마라, 나심 니콜라스 탈레브 저, 이건 역, 중앙북스, 2019
한겨례신문-벤포드법칙
일상과학위키-벤포드법칙
생일문제
More
| 2021/09/24 06:30 | |
| 2020/06/18 11:34 | |
| 2020/06/07 14:03 | |
| 2020/05/28 10:29 | |
| 2020/05/12 09:03 | |
| 2020/05/07 09:27 | |
| 2020/04/29 10:52 | |
| 2020/04/20 11:12 | |
| 2020/04/16 15:23 | |
| 2020/04/15 07:21 | |
| 2020/04/11 01:41 | |
| 2020/04/08 06:49 | |
| 2020/04/01 00:55 | |
| 2020/03/21 13:43 | |
| 2020/03/20 11:53 | |
| 2020/03/15 11:11 | |
| 2020/03/07 07:35 | |
| 2020/03/01 16:09 | |
| 2020/02/29 04:52 | |
| 2020/02/29 04:52 | |
| 2020/02/29 04:52 | |
| 2020/02/29 04:52 | |
| 2020/02/29 04:52 | |
| 2020/02/29 04:49 | |
| 2020/02/06 12:58 |
Discussion