shrinkage methods

라쏘? 로지스틱? 회의에서 당당하게, 수식없이 기초개념부터
best subset vs LASSO

«ELS»
subset selection

• discrete process : variables are either ratained or discarded
• often exhibits high variance, and so doesn't reduce the prediction error of the full model

Shrinkage methods are more continuous, and don't suffer as much from high variability

constrains or regularize

계수 추정치들을 수축하는 것은 추정치들의 분산을 상당히 줄일 수 있는 것으로 밝혀져 있다.

«CASI»
subset selection은 discrete process → high variance & doesn't reduce the prediction error of the full model
Roughly speaking, MLE는 nearly 최소 분산을 가지는 nearly unbiased 추정치를 제공
Again speaking roughly, unbiasedness는 수많은 parameters를 추정해야 하는 때에는 unaffordable luxury가 될 수 있음
~James-Stein Estimator

«CASI»
Ridge regression
standardize → $ \beta_i $ comparable scales.
$ \hat{\beta}(\lambda) = ( S + \lambda I)^{-1} X' y = ( S + \lambda I)^{-1} S \hat{\beta} $, $ S = X'X, \hat{\beta} = S^{-1} X' y $ (*)
penaliazed least squares; penalized likelihood; maximized a-posteriori probability(MAP); regularization

«ESL»
(*) ⇒ linear function of y
The solution adds a positive constant to the diagonal of $ X^TX $ before inversion.
⇒ X'X가 full rank 아니라도 problem을 nonsingular 로 만들어줌.

shrinkage panelty는 절편 $ \beta_0 $ 에는 적용X - 수축하고자 하는 것은 반응변수에 대한 각 변수의 추정된 연관성이지, $ x_{ij} = 0 $ 일 때 단순히 평균 반응변수 값의 측또인 절편을 수축하고자 하는 것은 아님. X의 열들을 평균이 0이 되도록 중심화하면 추정된 절편은 $ \hat{\beta_0} = \bar{y} = \sum y_i/n $의 형태가 된 것.

일반적인 LSE 추정치들은 스케일에 변동X : $ cX_j $ 이면 추정치가 1/c
그러나 ridge regression에서는 스케일링에 따라 달라짐 : $ \tilde{x}_{ij} = {x_{ij}\over{\sqrt{{1\over{n}}\sum(x_{ij}-\bar{x}_{j})^2}}} $ standardize (표준편차로 나누기)

bias-variace trade-off
일반적으로 반응변수와 설명변수의 상관관계가 선형에 가까운 경우 최소제곱 추정치는 낮은 bias를 가질 것이지만, 훈련 데이터의 작은 변화가 추정치를 크게 변화시킬 수 있으므로 분산은 높을수도.

2^p 개 best subset selection에 비해 계산상의 장점

p개 설명변수 모두를 포함함.

: assume that noise $ \epsilon $ is iid Normal.
$ \hat{\beta} \sim N_p(\beta, \sigma^2S^{-1} ) $
bayesian prior $ \beta \sim N_p (0, {\sigma^2\over\lambda}I) $ makes $ E\{\beta|\hat{\beta}\} = (S+\lambda I)^{-1}S\hat{\beta} $

SVD of the centered input matrix X : $ X = UDV^T $
$ X \hat{\beta}^{ls} = X(X^TX)^{-1}X^Ty = UU^Ty $, ls : least squares fitted vector
⇒ $ U^Ty $ : coordinates of y with respect to the orthonormal basis U
$ X \hat{\beta}^{ridge} = X(X^TX+\lambda I)^{-1} X^Ty = UD(D^2+\lambda I)^{-1}DU^Ty = \sum^p u_j {d_j^2 \over d_j^2+\lambda} u_j^Ty $
⇒ $ {d_j^2 \over d_j^2+\lambda} \leq 1 $ ⇒ shrink
small value of $ d_j^2 $ : X의 columns space direction 분산이 적다는 뜻 → 이 방향을 '더' 많이 줄여줌
(the SVD of the centered matrix X is another way of expressing the principal components of the variables in X
sample covariance matrix $ S = X^TX/N $ → $ X^TX = VD^2V^T $ → $ Var(z_1) = Var(Xv_1) = d_1^2/N $($z_1=Xv_1=u_1d_1 $, z_1 : 1st principal component)

$ l_2 $ penalty 대신 $ l_1 $ penalty ⇒ no closed form expression

정확히 0이됨. - sparse model(변수의 일부만 포함하는 모델) - 해석하기 쉬움

minimize $ { \sum ( y_i - \beta_0 - \sum \beta_j x_{ij} )^2 } s.t. \sum I(\beta_j \neq 0 ) \leq s $ s개의 계수만이 0이 아닌 값이 될 수 있다는 제한조건.
ridge : s.t. $ \sum \beta_j^2 \leq s $
lasso : s.t. $ \sum |\beta_j| \leq s $
( $ \lambda $ 에 대해 s가 존재, 1-1 correspondence )
⇒ ridge와 lasso 는 best subset의 풀기 힘든 문제를, 풀기 쉬운 문제로 대체한 계산 가능한 대안.

그림 출처 : ESL

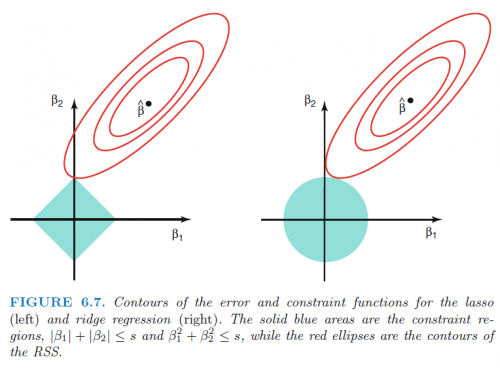
그림출처
변수가 2개일 때. 오차의 등고선(동일한 RSS)과 constraint function. $ \hat{\beta} $는 LSE.

일반적으로 lasso는 비교적 적은 수의 설명변수가 상당히 큰 계수를 가지고 나머지 변수들은 계수가 아주 작거나 0일 설정에서 성능이 더 나을 것이라 기대할 수 있음
ridge는 반응변수가 많은 설명변수들의 함수이고 그 계수들이 거의 동일한 크기일 때 성능이 더 좋을 것.

회귀에 대한 베이즈 관점은 계수 벡터 $ \beta $ 가 어떤 prior distribution $ p(\beta) $를 가진다고 가정.
likelihood : $ f(Y | X, \beta) $
posterior : $ p(\beta|X,Y) \propto f(Y|X,\beta) p(\beta|X) = f(Y|X,\beta)p(\beta) $
assume that $ p(\beta) = \prod g(\beta) $
⇒ g가 평균 0, 표준편차가 $ \lambda $ 의 함수인 Gaussian dist이면, $ \beta $ 의 posterior mode는 ridge의 해
g가 평균 0, scale parameter가 $ \lambda $ 의 함수인 double-exponential, Laplace dist 이면,$ \beta $ 의 posterior mode는 lasso의 해

Cross Validation

※ elestic net penalty
$ \lambda \sum (\alpha \beta_j^2 + (1-\alpha)|\beta_j|) $