Neural Network
인공신경망? 딥러닝? 회의에서 당당하게, 수식없이 알아보자
과적합 가능성, 해석X, 최후의 수단?
역사 : http://solarisailab.com/archives/1206
«PRML»
선형결합(회귀,분류모델) 유용한 해석적/계산적 성질이 있지만, 차원의 저주로 인해 실제적으로 사용하는 데 있어서 한계가 존재
큰 스케일의 문제에서 사용하기 위해서는 기저 함수가 데이터를 바탕으로 적응되도록 하는 것이 필요.
매개변수적인 기저함수를 사용하고 해당 매개변수값을 훈련 중에 조절.
사실 다층 퍼셉트론이라는 용어는 부적합. perceptron (불연속) 여러개가 모인 것이 아니라, 로지스틱 회귀 모델 여러층이 모인 것이기 때문. (미분 가능성)
SVM과 같은 일반화 성능을 가지면서도 결과 모델이 훨씬 더 작아서 계산이 빠르다는 장점
※ 활성화 함수가 선형이면, hidden layer 없는 동일 네트워크로 치환 가능. 연속적 선형 변환들로 구성된 변환은 그 자체가 선형변환이기 때문.
universal approximator : 선형 출력값을 가지는 2계층 네트워크(input/hidden 1) 는 충분히 많은 수의 hidden layer가 주어지기만 한다면 밀집된 입력 영역에 대한 모든 연속 함수를 임의의 정확도로 근사할 수 있음.
여러 가지의 서로 다른 w의 선택이 입력에서 출력으로의 같은 사상을 표현할 수 있음
NN을 성공적으로 사용하기 위해 global minimum을 찾는 것이 반드시 필요하지는 않을 수 있음
perceptron
perceptron : 1957년 고안
Artificial neuron, 다수의 신호를 입력으로 받아 하나의 신호를 출력
논리회로 : AND, NAND, OR 표현할 수 있음
$ (1, x_1,\ldots,x_n) \xrightarrow[\text{weights}]{w_0, w_1,\ldots,w_n} \sum w_ix_i $ → 1 or 0
step function
hyperplane으로 구분되는 두 개의 공간을 분리하는 역할
활성화 함수activation function
입력신호의 총합이 h(x)를 통해 변환
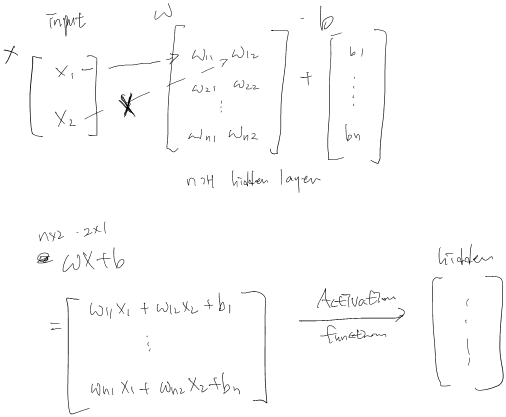
$ y = h ( XW+b ) $
출력 = 활성화함수( 입력*가중치 + 편향)
step function : S자 모양의 함수
sigmoid function : step 대신 sigmoid? 미분 위해서. step을 잘 근사한 smooth
(기술적으로 sigmoid는 함수의 모양을 지칭, logistic은 함수 자체를 가리키는 말)
ReLu(Rectified Linear Unit)
tanh
Neural Network
XOR(배타적 논리합)
둘 중 하나만 True인 연산. 단순 퍼셉트론으로는 불가능
직선 하나로는 불가능, 직선 제약을 없애면 가능
다층 퍼셉트론, 층을 쌓아서 가능. 뇌의 구조는 복잡. ANN으로 뇌를 묘사할 때는 여러 개의 연속된 층으로 추상화하는 것이 일반적
입력층, 은닉층, 출력층
identity function
softmax function (분류)
batch : 하나로 묶은 입력 데이터
mini-batch : 훈련 데이터 중 일부를 무작위로 꺼내고(mini-batch), 그 미니배치에 대해서 경사법으로 매개변수를 갱신
손실함수
MSE mean squared error
CEE cross entropy error
정확도를 지표로 삼으면 안되는 이유? 미분값이 대부분의 장소에서 0이 됨
- 정확도는 매개변수 조금 조정하게 되면 개선되지 않고 일정하게 유지.. discrete
- 손실함수는 연속적으로 변함
계산법
w의 차원을 W라고 할 때(매개변수 숫자),
2차 근사
Taylor expansion → hessian : W(W+3)/2 개의 독립적 원소를 가지게 됨 → O(W^2)
각각이 O(W) 단계만큼을 필요로 하는 함수 계산을 O(W^2) 만큼 해야 함 → 계산 O(W^3)
Gradient Descent
기울기정보 : O(W^2)
함수가 가장 빠르게 증가할 수 있는 방향
step size: 과학보다는 기술(art)에 가깝다.
vs Newton Mothod
https://qastack.kr/stats/253632/why-is-newtons-method-not-widely-used-in-machine-learning
2차 미분은 복잡하고, 계산이 많음
stochastic : 1) 데이터 상의 중복을 훨씬 더 효율적으로 처리. (ex. 모든 데이터 2배로 늘리면, 오차 함수 *2 한 것과 동일. 결과적으로 같음)
2) local minimum에서 탈출할 가능성이 높아짐. 전체 데이터 집합에 대한 오류 함수의 임계점은 보통 개별 데이터 포인트에 대해서는 임계점이 아닐 수도 있기 때문.
SGD
대부분의 오류함수는 더할수있는additive 속성을 가지고 있음. 즉, 데이터 전체에 대한 오류값이 각각 데이터 포인트에 대한 오류값의 합과 같다.
이럴 때는 한번 반복문을 돌 때마다 데이터 포인트 한 개에 대한 gradient를 계산.
back-propagation
https://www.offconvex.org/2016/12/20/backprop/
계산적 효율성.
W가 충분히 큰 경우, 오류함수 계산에 O(W) 만큼 연산 필요.
역전파를 사용하지 않고 오류함수 미분값을 계산할 수 있는 한 가지 방법은 유한차분법
수치 미분을 할 경우 문제점은 계산복잡도가 O(W)에 비례한다는 성질이 사라지게 된다는 것. 각각의 feed-forward 단계는 O(W) 만큼 계산을 필요, NW 상에서 개별적으로 perturbation 해야 할 W개의 가중치가 존재. 전체 계산 복잡도 O(W^2)
수치미분을 이용한 계산에는 시간이 걸리지만, 구현이 간단
back-propagation of error은 기울기를 고속으로 구할 수 있다.
1. 입력 벡터에 대해 feed_forward를 수행하고 모든 뉴런의 출력값을 계산
2. 각 뉴런에 대해 오류값 계산
3. weight에 따라 오류값의 gradient를 계산해서 오류를 최소화하는 방향으로 weight 재조정
4. hidden layer의 오류값을 추정하기 위해 출력층의 오류값을 뒤로 전파(back-propagate)
5. 오류값의 기울기를 다시 구하고 같은 방식으로 hidden layer의 weight를 재조정.
실제계산
참고 Calculus
$ f : \mathbb{R}^n \rightarrow \mathbb{R} $
- 방향미분 : $ D_vf(p) = lim_{t\rightarrow0} { {f(p+tv)-f(p)} \over {t}} = {d\over{dt}}|_0 f(p+tv)$
- f의 그래프를 직선 p+tv 위에 한정하여 그렸을 때, 점 (p,f(p))에서 f의 그래프의 기울기
- 편미분계수 : 점 p 에서 f의 $ e_k $ 방향 미분계수 $ D_{e_k}f(p) $
- Gradient(기울기) 벡터 $ \nabla f(p) = (D_1f(p),\ldots,D_nf(p)) $
- 접평면의 기울기 벡터
- 접평면 가진다 ⇔ $ lim_{x\rightarrow p} { {f(x)-f(p)-a(x-p)} \over {|x-p|} } = 0 $ ,(p,f(p) ) 지나는 평면 : y= f(p) + a(x-p)
- let x-p = v, $ lim_{v\rightarrow0} { {f(p+v)-f(p)-a \cdot v}\over {|v|} } = 0 $ 인 a 존재
- ⇔ $ f(p+v) = f(p) + av + o(v) $ (미분가능)
- ⇔ $ D_vf(p) = a \cdot v $
- $ a=(a_1,\ldots, a_n) $ 이면, $D_if(p) = D_{e_i}f(p) = a \cdot e_i = a_i $
- ⇒ $ D_vf(p) = \nabla f(p) \cdot v $
- v가 단위벡터일 때, $ = |\nabla f(p)| \cdot cos \theta $ (내적), theta : v와 grad f(p) 이루는 각
- ⇔ $ |\nabla f(p) $ : (속도)변화 최대(+)/최소(-) 방향 ( cosine = 1 되어야 최대임 )
http://matrix.skku.ac.kr/math4ai/part2/
https://freshrimpsushi.tistory.com/1010
Discussion